graph TB A([Group 1]) --> B[Unit 1] A --> C[Unit 2] A --> D[Unit 3] E([Group 2]) --> F[Unit 4] E --> G[Unit 5] E --> H[Unit 6] I([Group 3]) --> J[Unit 7] I --> K[Unit 8] I --> L[Unit 9]
Note
Some minor changes have been made to this blog post, cleaning up some unclear and confusing language/phrasing, and adding additional resources for learning about multilevel regression.
Multilevel models (MLMs) are hard. Some part of the difficulty is due to the fact that multilevel data structures add an extra layer of complexity conceptually and mathematically, and therefore the appropriate model structure for this kind of data is also more complex. However, there’s plenty about them that just seems needlessly hard.
Oh would you like to make a multilevel model or a hierarchical model? But have you considered a generalized linear mixed effects model? What about a variance component model? WHAT DO YOU MEAN THEY’RE THE SAME THING?1! That can’t possibly be true. Why would anyone in statistics or the sciences make anything needlessly convoluted and use different names for the same concepts? Thankfully things are much simpler when it comes to discussing fixed and random effects. Just a couple concepts with precise meaning and usage in every field… Wait, what? Oh you’ve got be fucking kidding me.
So I thought I’d try and make things a little easier for anyone taking their first steps into this fresh hell, and for anyone (like me) that has a mushy, liquefied brain and needs a refresher any time they haven’t looked at something every single day for the last two years.
I’m not going to write a full introduction, or a detailed how-to for constructing multilevel models, because a) that sounds long as hell and b) there are much smarter people than I that have already done these things (resources are linked at the end of the post). This will just serve as a quick explainer of what MLMs are, when you need them, and the syntax for constructing the most basic (and most common) types of MLMs in R. The goal is to keep this relatively short and make it accessible for folks without intensive statistics backgrounds. Therefore, I will attempt to keep the notation to the minimum, explaining model structures and using examples to illustrate. I have included some notation, but I’ve kept it hidden to make this cheatsheet2 a little bit less intimidating. If you fancy your chances, you can expand the notation sections.
I won’t go into the details about fitting, interpreting, and validating multilevel models here, but I will possibly turn this into a series, and if so I will get in to it in the next blog post. LFG!!!
What are Multilevel Models?
A common feature of many real-world questions that practitioners might study is that there are multiple “levels” around which the data is structured. A dataset may contain observations at a population-level, with a higher-level variable that specifies a group that those observations belong to (for example, patients being treated by a certain doctor or in a certain hospital, or political parties operating in different countries). Figure 1 below is a visual representation of how multilevel data might be structured.
Assuming that the grouping variable is relevant to the outcome being studied, this means that some observations will be correlated with each other, or clustered around the groups they belong to, which invites bias into any model that doesn’t account for this clustering. Multilevel models are regression models that handle data which is structured in groups3.
Notation
There are a few different ways that you might see multilevel models represented notationally, but when talking about the most general form of MLMs, the easiest way is using matrix notation:
\[Y = \alpha + X\beta + Z\gamma + \epsilon\]
where \(Y\) is a vector of observed values in the outcome variable, \(X\) is a matrix of predictors and \(Z\) is a matrix that refers to group-level deviation of the predictors (either in terms of the intercept or slope). \(\alpha\) refers to the global intercept, \(\beta\) represents the vector of fixed effects parameters, \(\gamma\) represents the vector of random effects, and \(\epsilon\) refers to the model’s error term.
However, I think it is generally easier to think about multilevel models in terms of the different levels that are being estimated in the model, and instead, throughout this blog post, I will give the level 1 and level 2 formulas for each model (we won’t go deeper than two levels for now, because I’m not a total monster).
It’s MLMs All The Way Down
There is lots of confusing and sometimes contradictory terminology that is used when talking about multilevel models.
Fixed & Random Effects
When discussing the ways that an effect can occur at different levels in a multilevel model, people will often refer to fixed and random effects. Fixed effects are those that are fixed across groups, or that are the same for every cluster, while the random effects are those that deviate between groups. The fixed and random effects could refer to either the intercept or the slope, as these can both vary between groups, and can in some cases both vary at the same time.
However, as Andrew Gelman has argued, these terms are sometimes used to refer to slightly different things, and this can lead to some confusion. So whenever you see someone refer to fixed or random effects, be aware that there may be some variance in how these terms are being used.
An alternative terminology, that possibly carries less confusion, is population- and group-level effects. When the variable is constant across groups/clusters and the effect varies at a unit-level (fixed-effect), this is referred to as a population-level effect. However, when the variable’s effect varies across groups/clusters (random-effect) then it is a group-level effect.
For the remainder of this blog post I will use this population- and group-level terminology.
Linear Mixed Models vs Multilevel Models
There are some slight differences between what a linear mixed model might refer to4, and what a hierarchical or multilevel model5 might refer to, but on the whole I think it is safe to treat them (generally speaking) as the same thing, with an understanding that multilevel models are any models where there are grouping structures that lead to the data violating the independence assumption, and hierarchical grouping structures are just one type of such structure.
An example of a context where you might see a grouping structure that isn’t hierarchical/nested is data where individuals are measured repeatedly, like, for example, a dataset containing repeated polling of individual’s views on a political candidate or issue (panel data). In this case, there is no hierarchical structure, but the grouping structure is the individual.
Multilevel Model Syntax in R
The good thing about the R syntax I detail in this section is that it is the same for lme4, the main package for frequentist multilevel models, and the same for brms and rstanarm, two of the most popular packages for computing Bayesian multilevel models.
The basic structure of multilevel models in R is very similar to typical lm() formulae, using y ~ x1 + x2 ... + xn, but in addition to this, the MLM syntax accounts for a grouping structure in the data using the pipe: |.
Below are some examples of simple multilevel model structures, where x refers to a unit-level variable and g refers to the group variable. Figure 2 demonstrates visually the multilevel models that will be covered.
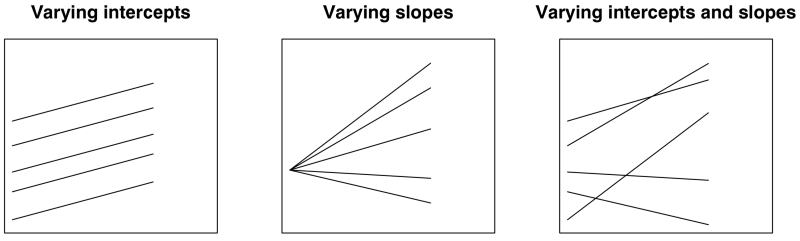
Varyings Intercepts
The simplest kind of model you can specify with a grouping structure is one which models a grouping structure with deviance from the global intercept, but no unit-level predictors. This means that the intercept is allowed to vary between groups (for example, patient outcomes in different hospitals), around the mean intercept of all groups (the global intercept). This is often referred to as a null model, or a varying (random) intercepts model.
This can be specified as such:
y ~ 1 + (1|g)The 1 outside of the brackets here specifies the fixed mean global intercept, and the (1|g1) specifies that the grouping structure produces intercepts that vary for each group.
Notation
\[y_{ij} = \alpha_{j} + \epsilon_{ij}\]
\(\alpha_{j}\) refers to the intercept (\(\alpha\)) for every group (\(j\)), meaning that every group \(j\) has its own intercept. The formula for \(\alpha_{j}\) can be written as follows:
\(\alpha_{j} = \gamma_{00} + \mu_{0j}\)
This formula is the group level intercept variance, explaining the \(j\)th group’s deviation from the mean global intercept, with \(\gamma_{00}\) representing the mean global intercept, and \(\mu_{0j}\) representing the deviance from the mean intercept.
Adding Population Effects
While the previous model only included a group-level effect that caused deviance from the global intercept, there was no population-level effect in the model. If we add a population-level effect \(x\) to the model, we get the following:
y ~ x + (1|g)This is a pretty typical multilevel model that you’ll see plenty of examples of in the real-world and find plenty of use for when implementing MLMs yourself.
Notation
\[y_{ij} = \alpha_{j} + \beta_{1j}x_{ij} + \epsilon_{ij}\]
This is the level one formula for the value of \(y\) indexed by \(i\) units and \(j\) groups.
\(\alpha_{j}\) refers to the intercept (\(\alpha_{}\)) for every group (\(j\)), meaning that every group \(j\) has its own intercept. The formula for \(\alpha_{j}\) can be written as follows:
\(\alpha_{j} = \gamma_{00} + \mu_{0j}\)
And the formula for \(\beta_{1j}\) is:
\(\beta_{1j} = \gamma_{10}\)
These two formulas are the second level of the model, with \(\alpha_j\) explaining the \(j\)th group’s deviation from the global intercept, when there are varying intercepts, with \(\gamma_{00}\) representing the global_intercept, and \(\mu_{0j}\) representing the deviance from the mean intercept, and \(\beta_{1j}\) explaining the unit-level variance of \(x\), with \(\gamma_{10}\) representing the population-effect for the slope of \(x\).
Varying Slopes
Sometimes there will be an expectation that the grouping structure has no effect on the intercept, but that the slope will vary between groups (though this kind of model is generally less common). The following model structure will do the job, in those instances:
y ~ x + (0 + x|g)The default structure in multilevel modelling is to include a varying intercept, which is represented by the 1 that sits inside the brackets in the code, (1|g). If you don’t want to include a varying intercept, then a 0 is required to override this default.
While possibly less common than a varying intercepts model, I think it is also useful to understand how a varying slopes model is structured, in order to get a better understanding of how MLMs work both conceptually and technically.
Notation
If the intercepts are fixed and the slopes vary, then the formula would be slightly different to the one presented earlier:
\[y_{ij} = \alpha_j + \beta_{1j}x_i + \epsilon_{ij}\]
The differences lie in the second level formulas:
\(\alpha_j\) would be written as:
\[\alpha_j = \gamma_{00}\]
While the formulas for \(\beta_{1j}\) would be written as:
\[\beta_{1j} = \gamma_{10} + \mu_{1j}\]
The difference here is that the \(\alpha_j\) no longer has a \(\mu_{0j}\) term, because there is no group-level deviation around the global intercept, while \(\beta_{1j}\) has a \(\mu_{1j}\) term, representing the \(j\)th group’s deviation from the global mean of the slope.
Varying Intercepts & Slopes
And once you’ve figured out how to build a model that varies either the intercepts or the slopes, you can then let it all hang out and just let the groups do whatever the hell they want, in the form of both varying intercepts AND slopes.
The syntax for this kind of structured madness is as follows:
# correlated intercepts and slopes
y ~ x + (1 + x|g)
# uncorrelated intercepts and slopes
y ~ x + (x||g)I think the previous section, detailing the structure and syntax of a varying slopes model, really helps figure things out when presented in conjunction with this model structure. The incremental changes that lead to different types of models should help to identify which components do what.
Notation
As you might expect, the formula for a multilevel model with both varying intercepts and slopes will look like a combination of the previous two examples:
\[y_{ij} = \alpha_{j} + \beta_{1j}x_i + \epsilon_{ij}\]
where \(\alpha_{j}\) (the intercept) can be expanded as:
\[\alpha_{j} = \gamma_{00} + \mu_{0j}\]
and where \(\beta_{1j}\) (the slope) can be expanded as:
\[\beta_{1j} = \gamma_{10} + \mu_{1j}\]
Hopefully by now the multilevel model structure is starting to make some sense. The distinction between the previous models and this model formula, that makes it a varying intercepts and slopes model, is the fact that there is a term for the variance from the global mean in both the second-level formula for the intercept (\(\mu_{0j}\)) and the slope ((\(\mu_{1j}\))).
Conclusion
So I’ve laid out the basic structure of multilevel modelling, hopefully making it easier to figure out the syntax in R, and build some simple MLMs. Things can quickly get more and more complicated when you start adding multiple grouping structures, or as you add multiple predictors and interactions, but the basics laid out in this article should be enough to get you started building multilevel models. In future blog posts (making some strong assumptions about my commitment to this bit) I will take a look at how to fit and interpret these simple multilevel models, using simulated data.
There’s lots of ways you can specify a multilevel model that involve vast complex grouping structures nested between each other or crossed with population-level effects. However, more often than not, I think you will get away with just using a simple structure, particularly the varying intercepts model. This will get you most of the way there, especially while you’re learning your way with multilevel modelling. Once you’re more comfortable with the idea conceptually and technically? You can start to make a real mess!
Given how complex things can get with MLMs, this cheatsheet is obviously only scratching the surface. Therefore, in the interest of not leaving anyone with a thirst-for-the-learn hanging, here’s a few resources to help along the way:
- Shaw & Flake - Introduction to Multilevel Modelling
- Gelman & Hill - Data Analysis Using Regression and Multilevel/Hierarchical Models
- Gelman et al. - Applied Regression and Multilevel Models6
- brms Vignettes
- Heiss - A Guide to Working with Country-Year Panel Data and Bayesian Multilevel Models
- Clark - Mixed Models with R
- Magnusson - Using R and lme/lmer to Fit Different Two- and Three-Level Longitudinal Models
Acknowledgments
Preview image by Patrick Baum on Unsplash.
Support
If you enjoyed this blog post and would like to support my work, you can buy me a coffee or a beer or give me a tip as a thank you.
Footnotes
There are some minor distinctions, but the terms are often used interchangeably.↩︎
Does a blog post get to call itself a cheatsheet?↩︎
There are alternative ways to handle clustered data, such as cluster-robust standard errors, but I won’t cover that here. If you’re interested in learning about these methods, I’d recommend the discussion in Chapter 3 of Introduction to Multilevel Modelling, or this overview that is linked in the discussion.↩︎
A linear mixed model can refer to any model that contains a group/clustering structure, and it does not have to be a group that is organised hierarchically, or nested.↩︎
Hierarchical/multilevel models suggest that there might be a vertical hierarchy that explains the grouping structure in the data, for example, student test results are nested within a class or school grouping structure.↩︎
ARMM hasn’t been published (released?) yet, but it is billed as the updated and expanded second edition of Gelman & Hill’s book. It’s worth keeping an eye out for when this is released, because I’m sure it will be an excellent resource.↩︎
Reuse
Citation
For attribution, please cite this work as:
Johnson, Paul. 2022. “A Cheatsheet for Building Multilevel Models
in R.” November 1, 2022. https://paulrjohnson.net/blog/2022-11-01-multilevel-model-r-cheatsheet/.